With “What Type of Number is -1/2” at the forefront, this paragraph opens a window to an intriguing start, inviting readers to embark on a storytelling journey filled with unexpected twists and insights. As we delve into the world of numbers, we will discover that -1/2 is a fascinating entity that defies simple categorization.
Delving deeper into the topic, we will explore the concept of rational numbers and how -1/2 fits into this category. We will also discuss the difference between rational and irrational numbers, providing examples to solidify our understanding.
Understanding the Nature of
1/2
1/2

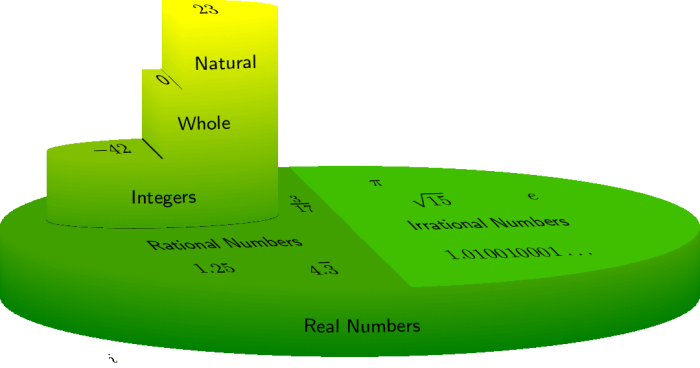
The number -1/2 belongs to the category of rational numbers. Rational numbers are numbers that can be expressed as a fraction of two integers, where the denominator (the bottom number) is not zero. In the case of -1/2, the numerator (the top number) is -1 and the denominator is 2.
Rational numbers are distinct from irrational numbers, which cannot be expressed as a fraction of two integers. For example, the square root of 2 is an irrational number because it cannot be written as a fraction of two whole numbers.
The decimal representation of an irrational number goes on forever, without repeating any pattern.
On the number line, -1/2 is located halfway between -1 and 0. This can be visualized as a point on the line that is equidistant from both -1 and 0.
Operations Involving
So, -1/2 is a rational number because it can be expressed as a fraction of two integers. Speaking of fractions, have you tried branch and vine hand soap ? It’s a great way to keep your hands clean and smelling fresh.
Anyway, back to -1/2. Since it’s a rational number, it can also be represented as a decimal, which is -0.5.
1/2

In this section, we will explore various mathematical operations involving the number -1/2. We will demonstrate how to perform addition, subtraction, multiplication, and division operations with -1/2, providing step-by-step examples for clarity.
Addition and Subtraction
When adding or subtracting -1/2, we follow the same rules as adding or subtracting any other fraction. To add two fractions with different denominators, we first find a common denominator and then add the numerators.
- Example: 1/4 + (-1/2) = (1/4) + (-2/4) = -1/4
- Example: (-3/8) – (-1/2) = (-3/8) + (4/8) = 1/8
Multiplication
To multiply a fraction by a whole number or another fraction, we simply multiply the numerators and denominators.
- Example: (-1/2) x 3 = (-1 x 3) / (2 x 1) = -3/2
- Example: (-1/2) x (-3/4) = (-1 x -3) / (2 x 4) = 3/8
Division
To divide a fraction by a whole number or another fraction, we invert the divisor (flip the numerator and denominator) and multiply.
- Example: (-1/2) ÷ 2 = (-1/2) x (1/2) = -1/4
- Example: (-1/2) ÷ (-3/4) = (-1/2) x (-4/3) = 2/3
The following table summarizes the operations and their results:
| Operation | Result |
|---|---|
| 1/4 + (-1/2) | -1/4 |
(-3/8)
|
1/8 |
| (-1/2) x 3 | -3/2 |
| (-1/2) x (-3/4) | 3/8 |
| (-1/2) ÷ 2 | -1/4 |
| (-1/2) ÷ (-3/4) | 2/3 |
Properties of
1/2
1/2
The number -1/2 possesses several distinct properties that define its mathematical nature and behavior. These properties play a crucial role in various mathematical operations and real-life applications.
Negative Number, What type of number is -1/2
-1/2 is a negative number, meaning it lies to the left of zero on the number line. Negative numbers represent values less than zero and are typically used to indicate quantities or measurements that are below a reference point or baseline.
Less than Zero
-1/2 is less than zero. This property stems from its negative nature. Any negative number is considered smaller than zero, as it represents a value that is below the zero mark.
Additive Inverse
-1/2 has an additive inverse of 1/2. The additive inverse of a number is the number that, when added to the original number, results in zero. In the case of -1/2, its additive inverse is 1/2, as (-1/2) + (1/2) = 0.
Reciprocal
The reciprocal of a number is the number that, when multiplied by the original number, results in one. The reciprocal of -1/2 is -2, as (-1/2) – (-2) = 1.
Real-Life Examples
- A temperature of -1/2 degrees Celsius represents a temperature that is half a degree below zero.
- A debt of -1/2 rupees indicates a financial obligation that is half a rupee less than zero.
- A movement of -1/2 meters to the left represents a displacement of half a meter in the opposite direction from the starting point.
Applications of
1/2
1/2

The value -1/2, representing the negative one-half, finds practical applications in various fields, including physics, engineering, economics, and everyday situations. It serves as a valuable tool for solving problems and representing real-world scenarios.
Physics
-1/2 appears in the formula for projectile motion, which calculates the vertical displacement of an object under the influence of gravity. It represents the acceleration due to gravity, which is a constant value on Earth.
Engineering
-1/2 is used in structural engineering to calculate the bending moment in a beam. It represents the moment arm, which is the perpendicular distance from the point of application of a force to the neutral axis of the beam.
Economics
-1/2 is employed in the calculation of elasticity, a measure of how responsive a demand or supply curve is to changes in price. It represents the slope of the demand or supply curve, indicating the percentage change in quantity demanded or supplied for a given percentage change in price.
Everyday Situations
-1/2 can be used to represent a half-filled container, a discount of 50%, or a ratio of 1 to 2. It is a versatile value that can be applied to a wide range of scenarios.
FAQ Corner: What Type Of Number Is -1/2
Is-1/2 a positive or negative number?
-1/2 is a negative number because it is less than zero on the number line.
What is the reciprocal of-1/2?
The reciprocal of -1/2 is -2, which means -1/2 multiplied by -2 equals 1.
Can-1/2 be expressed as a percentage?
Yes, -1/2 can be expressed as a percentage: -50%.